Research

My research is focused on the intersection between applied math and condensed matter physics with a particular focus on electronic properties of materials. Most recently, I’ve been interested in understanding electron-electron interactions in moiré materials (in particular twisted bilayer graphene). Previously, I worked on sparse basis construction for insulating materials. A list of my publications is below.

Moiré Materials

When two periodic patterns are twisted relative to each other, a large scale pattern, called a moiré pattern, is formed. Recently, it was discovered that by placing two thin sheets of a material on top of each other with a relative twist, the interplay between the small scale atomic configuration and the large scale moiré pattern leads to remarkable behaviors such as correlated insulators and superconductivity. These behaviors are due in part to the fact that the interactions between the two scales (atomic and moiré) can suppress the kinetic energy of the electrons making electron-electron repulsion dominant. In my work, I have studied the role of electron-electron repulsion in twisted bilayer graphene and its implications for the ground states.

Sparse Basis Construction

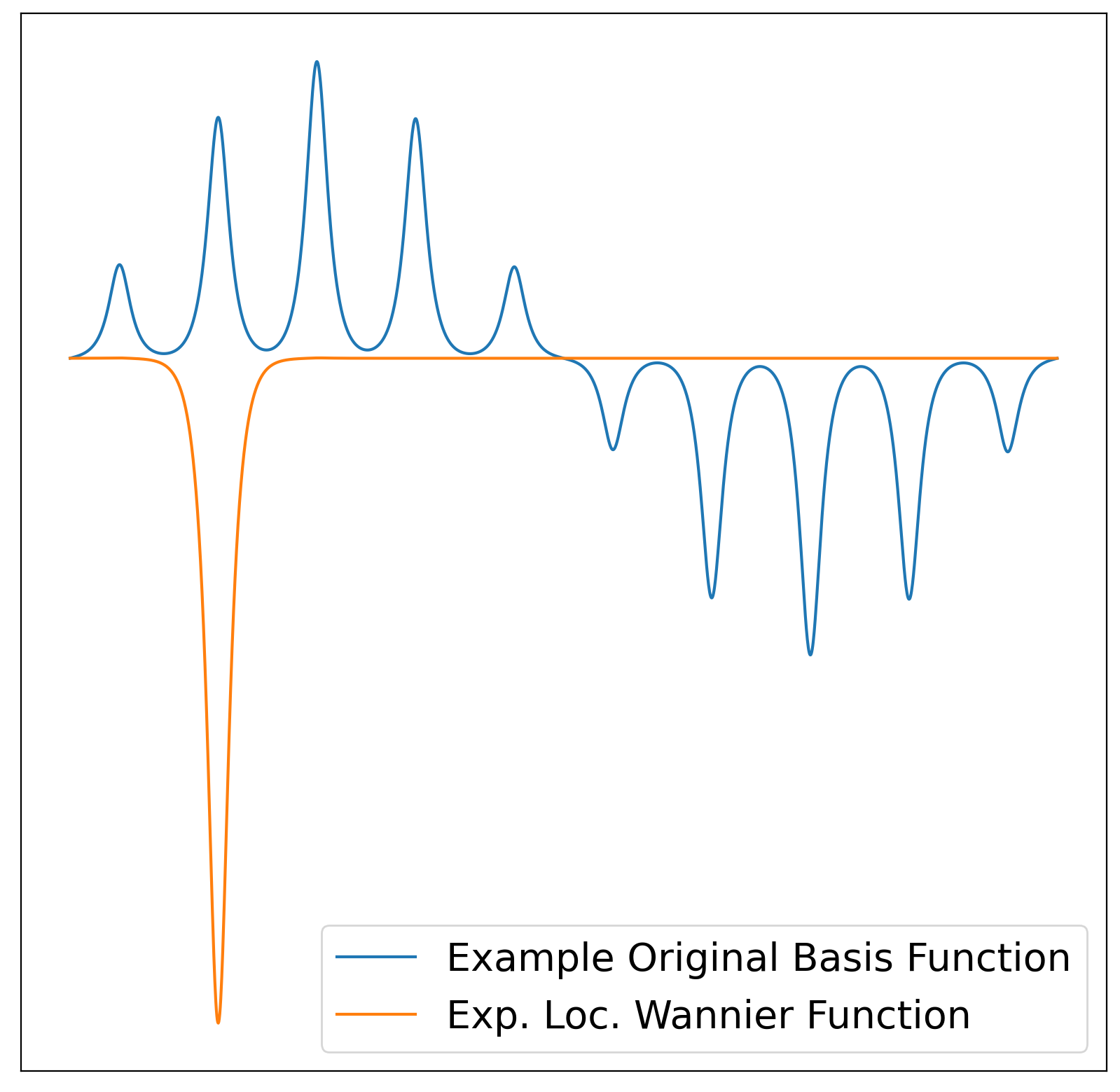Given a subspace of a vector space, a standard step in most algorithms is to construct an orthogonal basis for this subspace. Not all orthogonal bases are equally well suited for computation however. For studying systems with local interactions, bases which decay quickly in space lead to sparse equations which drastically speed up calculation. In electron structure theory, orthogonal bases which decay exponentially quickly in space are called exponentially localized (generalized) Wannier functions (ELWFs). In my work, I proposed an algorithm for constructing ELWFs and proved its correctness for a large class of subspaces (Left: A low energy eigenfunction of -Δ + V and an ELWF which is contained in the low energy eigenspace).

Publications

[15]	Kevin D Stubbs, Michael Ragone, Allan H MacDonald, and Lin Lin. The many-body ground state manifold of chiral twisted bilayer graphene. in preparation, 2024.
[14]	Woochang Kim, Raehyun Kim, Kevin D Stubbs, Steve Louie, and Lin Lin. Dft based ab initio modelling of twisted bilayer graphene. in preparation, 2024.
[13]	Jianfeng Lu and Kevin D Stubbs. Algebraic localization of wannier functions implies chern triviality in non-periodic insulators. In Annales Henri Poincaré, pages 1--16. Springer, 2024.
[12]	Kevin D Stubbs, Simon Becker, and Lin Lin. On the hartree-fock ground state manifold in magic angle twisted graphene systems. arXiv preprint arXiv:2403.19890, 2024.
[11]	Abhijeet Alase, Kevin D Stubbs, Barry C Sanders, and David L Feder. Exponential suppression of pauli errors in majorana qubits via quasiparticle detection. arXiv preprint arXiv:2307.08896, 2023.
[10]	Fabian M Faulstich, Kevin D Stubbs, Qinyi Zhu, Tomohiro Soejima, Rohit Dilip, Huanchen Zhai, Raehyun Kim, Michael P Zaletel, Garnet Kin-Lic Chan, and Lin Lin. Interacting models for twisted bilayer graphene: A quantum chemistry approach. Physical Review B, 107(23):235123, 2023.
[9]	Simon Becker, Lin Lin, and Kevin D Stubbs. Exact ground state of interacting electrons in magic angle graphene. arXiv preprint arXiv:2312.15314, 2023.
[8]	Sarah Brandsen, Kevin D. Stubbs, and Henry D. Pfister. Reinforcement Learning with Neural Networks for Quantum Multiple Hypothesis Testing. Quantum, 6, 2022. [ DOI ]
[7]	Jianfeng Lu, Kevin D Stubbs, and Alexander B Watson. Existence and computation of generalized wannier functions for non-periodic systems in two dimensions and higher. Archive for Rational Mechanics and Analysis, pages 1--55, 2022.
[6]	Jianfeng Lu and Kevin D Stubbs. Algebraic localization implies exponential localization in non-periodic insulators. arXiv preprint arXiv:2101.02626, 2021.
[5]	Kevin D Stubbs, Alexander B Watson, and Jianfeng Lu. Iterated projected position algorithm for constructing exponentially localized generalized wannier functions for periodic and nonperiodic insulators in two dimensions and higher. Physical Review B, 103(7):075125, 2021.
[4]	Sarah Brandsen, Mengke Lian, Kevin D Stubbs, Narayanan Rengaswamy, and Henry D Pfister. Adaptive procedures for discriminating between arbitrary tensor-product quantum states. In 2020 IEEE International Symposium on Information Theory (ISIT), pages 1933--1938. IEEE, 2020.
[3]	Anna N Morozovska, Eugene A Eliseev, Kevin D Stubbs, Rama Vasudevan, Yunseok Kim, and Sergei V Kalinin. Phase diagrams of single-layer two-dimensional transition metal dichalcogenides: Landau theory. Physical Review B, 101(19):195424, 2020.
[2]	Wojciech Czaja, Benjamin Manning, James M Murphy, and Kevin Stubbs. Discrete directional gabor frames. Applied and Computational Harmonic Analysis, 45(1):1--21, 2018.
[1]	Zhenning Cai, Jianfeng Lu, and Kevin Stubbs. On discrete wigner transforms. arXiv preprint arXiv:1802.05834, 2018.